This post is translated from Chinese into English through AI.View Original
AI-generated summary
This is a summary of the revision of computer organization principles, focusing on arithmetic methods and arithmetic units. It covers topics such as number systems and encoding, representation and operations of fixed-point numbers, representation and operations of floating-point numbers, and arithmetic logic units (ALU). It also includes discussions on topics such as binary to decimal conversion, decimal to binary conversion, BCD codes, characters and strings, and parity check codes. The summary provides explanations and examples of various concepts and methods related to arithmetic operations in computer systems.
Chapter 2 Arithmetic Methods and Arithmetic Units#
Machine Code: The number represented in the machine, addressing the issues of positive and negative signs and decimal point operations in the computer.
Each bit of the binary code representing a decimal digit has a definite weight. Generally, 8421 code is used, where the weights of the four binary codes from high to low are 8, 4, 2, and 1. The values 0000, 0001, ..., 1001 represent 0, 1, ..., 9 respectively, with each digit satisfying binary rules internally, while the digits between satisfy decimal rules, hence this encoding is called "Binary Coded Decimal (BCD)".
Note! The value range of BCD code is from 0000 to 1001 (i.e., decimal 0 to 9)
Sometimes, performing addition or subtraction on BCD code may yield values outside this range, requiring manual adjustment to obtain correct results.
To implement BCD arithmetic operations in the computer, the operation results need to be corrected, and the correction rule for addition is:
If the sum of two one-digit BCD codes is less than or equal to (1001)~2~, i.e., (9)~10~, no correction is needed;
Example 1 ① 1+8 = 9 0 0 0 1+ 1 0 0 0 —————————— 1 0 0 1 No correction needed
If the sum is greater than or equal to (10)~10~, a correction of +6 must be performed, and a carry is generated, which can occur during the first addition (Example 1 ③) or during correction (Example 1 ②).
1. Representation Methods for Characters and Strings#
Symbol data: Character information is represented by data, such as ASCII.
Character representation method ASCII: Uses one byte for representation, with the lower 7 bits for encoding (128), and the highest bit as a parity bit, as shown in the image
Storage method for strings: Occupies multiple contiguous bytes in main memory, each byte stores one character.
There are 3755 first-level Chinese characters and 3008 second-level Chinese characters.
Internal code for Chinese characters: The internal code for storing, exchanging, and retrieving Chinese character information, composed of two bytes, with the highest bit of each byte being 1 (distinguishing from English characters).
Chinese character glyph code: The dot matrix of Chinese character shapes.
Let x=(x~0~ x~1~.x~n-1~) be an n-bit word, then the even parity bit C is defined as: C=x~0~ ^ x~1~ ^ x~2~ ^ ... ^x~n-1~, where ^ represents bitwise addition, indicating that C=0 only when x contains an even number of 1s, otherwise C=1. It can only detect errors but cannot correct them. Similarly, odd parity can be defined.
Odd parity: C=0 only when there is an odd number of 1s, otherwise C=1.
2.2 Representation and Operations of Fixed-Point Numbers (Key Point)#
Fixed-point decimal x~n~.x~n-1~x~n-2~…..x~0~, x is the true value
\begin{cases}
x, & \text{0 ≤ x < 1 i.e., x is positive} \\
1-x, & \text{-1 < x ≤ 0 i.e., x is negative}
\end{cases}$$
Range is 2^-n^-1~1-2^-n^
eg:
x = +0.1001, [x]_{sign} = 0.1001
x = -0.1001, [x]_{sign} = 1-(-0.1001)=1.1001
**Fixed-point integer x~n~x~n-1~x~n-2~…..x~0~**, x is the true value
$$[x]_{sign} =
\begin{cases}
x, & \text{0 ≤ x < }2^n i.e., x is positive\\
2^n-x, & \text{-2}^n<x≤ 0 \text{ i.e., x is negative}
\end{cases}$$
Range is 1-2^n^~2^n^-1
eg:
x = +1001, [x]_{sign} = 01001
x = -1001, [x]_{sign} = 2^4^+1001=11001
**There is a distinction between positive 0 and negative 0!!**
#### 2. One's Complement Representation
**Definition**
- **Positive numbers** are represented the same as in sign-magnitude and two's complement.
- **Negative numbers** have a **sign bit of 1**, and the **value bits** are obtained by **inverting the value of the sign-magnitude representation**.
- The circuit is easy to implement, as the output of the flip-flop has a distinction between positive and negative.
To find the complement of the mantissa, the difference between one's complement and two's complement is that one additional 1 is added to the least significant bit, thus leading to the definition of one's complement.
**Fixed-point decimal x~n~.x~n-1~x~n-2~…..x~0~**, x is the true value
$$[x]_{one} =
\begin{cases}
x, & \text{0 ≤ x < 1 i.e., x is positive} \\
(2-2^{-n})+x, & \text{-1 < x ≤ 0 i.e., x is negative}
\end{cases}$$
eg:
X1=+0.1011011 , [X1]_{one} =0.1011011
X2= -0.1011011 , [X2]_{one} =1.0100100
**Fixed-point integer x~n~x~n-1~x~n-2~…..x~0~**, x is the true value
$$[x]_{one} =
\begin{cases}
x, & \text{0 ≤ x < }2^n i.e., x is positive \\
(2^{n+1}-1)+x, & \text{-2}^n<x≤ 0 \text{ i.e., x is negative}
\end{cases}$$
**One's complement representation has a distinction between positive 0 and negative 0!!**
#### 3. Two's Complement Representation
**Definition**
The two's complement of a positive number is the number itself, while the two's complement of a negative number is the original negative number plus the modulus (the original negative number is inverted except for the sign bit, then 1 is added). Computer operations are limited by word length, belonging to modular arithmetic. The greatest advantage of two's complement is that it converts subtraction into addition.
**Fixed-point decimal x~n~x~n-1~x~n-2~…..x~0~, modulo 2**
$$[x]_{two} =
\begin{cases}
x, & \text{0 ≤ x < 1 i.e., x is positive} \\
2+x, & \text{-1 < x ≤ 0 i.e., x is negative}
\end{cases}$$
eg: x= -0.1011, [x]_{two}=10+x=10.0000-0.1011=1.0101
y=-0.01111 [y]_{two}=10+y=10.00000-0.01111=1.10001
**Fixed-point integer x~n~x~n-1~x~n-2~…..x~0, modulo 2^n+1**
$$[x]_{two} =
\begin{cases}
x, & \text{2}^n {>x ≥ 0 i.e., x is positive} \\
2^{n+1}+x, & \text{0 ≥ x > -2}^n {i.e., x is negative}
\end{cases}$$
**Properties of Two's Complement:**
- The high bit indicates the sign
- For positive numbers, the two's complement mantissa is the same as the sign-magnitude representation
- Range -2^n^~2^n^-1 (fixed-point integers)
- **No distinction between positive zero and negative zero!!**
#### 4. Biased Representation
Used in exponent representation, characterized by **the biased representation and two's complement mantissa being the same, but the sign bits are opposite**.
Range: -2^n^~2^n^-1
eg: True value -1011111
Sign-magnitude representation is 11011111
Two's complement is 10100001
One's complement is 10100000
Biased representation is 00100001
#### 5. Summary
- **If x is positive, [x]_{sign} = [x]_{two} = [x]_{one}**
- **If x is negative**, **the sign bit of the sign-magnitude representation remains 1**, each bit of the integer's binary representation is inverted to obtain the one's complement, the sign bit remains unchanged, and the value bits have 1 added to the least significant bit to obtain the two's complement.
- **The mantissas of biased and two's complement representations are the same, but the sign bits are opposite**.
### 2. Operations on Fixed-Point Numbers (Key Point)
[Computer Organization Principles Fixed-Point Operations - Shifting, Addition, Subtraction, Multiplication, Division](https://blog.csdn.net/gl620321/article/details/106534016?utm_medium=distribute.pc_relevant.none-task-blog-baidujs_title-0&spm=1001.2101.3001.4242)
#### 1. Shift Operations on Fixed-Point Numbers
Shifting in computers refers to moving data relative to the decimal point (left or right), with the data moving while **the position of the decimal point remains unchanged**.
##### Shift for Signed Numbers
Left shift by 1: The absolute value of the true value corresponding to the machine number becomes twice the original.
Right shift by 1: The absolute value of the true value corresponding to the machine number becomes half the original.
During the shifting process, fill the empty positions:
- The negative number's value part remains the same as the true value 
##### Shift for Unsigned Numbers
- Logical left shift fills 0 in the low bits, discards the high bits
- Logical right shift fills 0 in the high bits, discards the low bits
eg:
01010011
Logical left shift: All bits participate in the shift operation, the high bit 0 is discarded, and the low bit is filled with 0: 10100110
Arithmetic left shift: The first 0 indicates the sign bit, this number is positive, the sign bit does not participate in the shift, the data being shifted is 00100110.
eg:
10110010
Logical right shift: All bits participate in the shift operation, the highest bit is filled with 0, and the lowest bit is discarded: 01011001
Arithmetic right shift: The highest bit does not participate in the shift, the sign bit indicates a negative number, the highest bit filled with 1 during the shift, and the lowest bit is discarded: 11011001
#### 2. Addition and Subtraction in Two's Complement
##### Addition in Two's Complement
Formula: $$ [x+y]_{two}=[x]_{two}+[y]_{two} (mod 2^{n+1}) \\
|x|<(2n-1) , |y|<(2n-1) , |x+y|<(2n-1) $$ The formula indicates that under modulo 2^n+1, **the sum of the two's complement of any two numbers equals the two's complement of the sum of those two numbers**.
Proof:
(1) x > 0, y > 0, then x+y > 0, since the sign-magnitude and two's complement representations of positive numbers are the same, so [x]_{two}+[y]_{two} = x+y = [x+y]_{two}
(2) x > 0, y < 0, then x+y > 0 or x+y < 0
**[x]_{two}= x,[y]_{two} = 2^n+1+y**
[x]_{two}+[y]_{two} = (x+y)+2^n+1 = [x+y]_{two} (mod 2^n+1)
(3) x < 0, y > 0, then x+y > 0 or x+y < 0
**[x]_{two}= 2^n+1+x,[y]_{two} = y**
[x]_{two}+[y]_{two} = (x+y)+2^n+1 = [x+y]_{two} (mod 2^n+1)
(4) x < 0, y < 0, then x+y < 0
**[x]_{two}= 2^n+1+x,[y]_{two} = 2^n+1+y**
[x]_{two}+[y]_{two} = 2^n+1+x + 2^n+1+y
= 2^n+1+( 2^n+1+x+y)
= [x+y]_{two} (mod 2^n+1)
eg: x=+1011 , y=-0101 , find x+y=?
Solution: [x]_{two} = **0**1011, [y]_{two} = **1**1011
[x]_{two} **0** 1 0 1 1
+ [y]_{two} **1** 1 0 1 1
————————————————
[x+y]_{two} **~~1~~ 0** 0 1 1 0
∴ x+y = +0110
1. The sign bit participates in the operation as part of the number.
2. Add under modulo 2n+1, meaning that any carry exceeding 2n+1 is discarded.
##### Subtraction in Two's Complement
To convert subtraction into addition, the formula needs to be proven:
$$ [x-y]_{two}=[x]_{two}-[y]_{two} = [x]_{two}+[-y]_{two} (mod 2^{n+1}) $$
[x-y]_{two}= [x]_{two}- [y]_{two}=[x]_{two}+[-y]_{two}
(Proof) To find [-y]_{two}, it needs to be proven that [-y]_{two} = [y]_{two} + 2^{-n} (meaning that [-y]_{two} equals [y]_{two} including the sign bit inverted, with 1 added to the least significant bit).
Since [x]_{two}+[y]_{two} = [x+y]_{two}
Thus, [y]_{two} = [x+y]_{two} - [x]_{two}
Also, [x-y]_{two} = [x+(-y)]_{two} = [x]_{two}+[-y]_{two}
Thus, [-y]_{two} = [x-y]_{two} - [x]_{two}
Therefore, [y]_{two} + [-y]_{two}
= [x+y]_{two} - [x]_{two} + [x-y]_{two} - [x]_{two}
= [x+y+x-y]_{two}-[x+x]_{two}
= [x+x]_{two} - [x+x]_{two}
= 0
Thus, [-y]_{two} = -[y]_{two} (mod 2^n+1)
**To find [-X]_{two}: invert each bit including the sign bit, and add 1 to the least significant bit.**
#### 3. Multiplication and Division of Fixed-Point Numbers
##### Multiplication Operation


##### Division Operation
**Restoring Remainder Method**: Subtract the divisor from the dividend,
If the result is greater than 0, the quotient is 1, and the remainder is shifted left by one position.
If the result is less than 0, the quotient is 0, restore the remainder, and shift the remainder left by one position.
Repeat the above operations until the precision of the quotient meets the requirements.
Non-restoring method (**Alternating Addition and Subtraction Method**)
- **First time**: If **the dividend and divisor have the same sign**, perform **dividend minus divisor**; if **the dividend and divisor have different signs**, perform **dividend plus divisor**.
- If **the remainder and divisor have the same sign**, **quotient is 1, shift the remainder left** and **subtract the divisor**; if **the remainder and divisor have different signs**, **quotient is 0, shift the remainder left** and **add the divisor**.
- The last bit of the quotient is always set to 1 (error 2^-n), and the remainder can be negative, no need to restore the remainder.
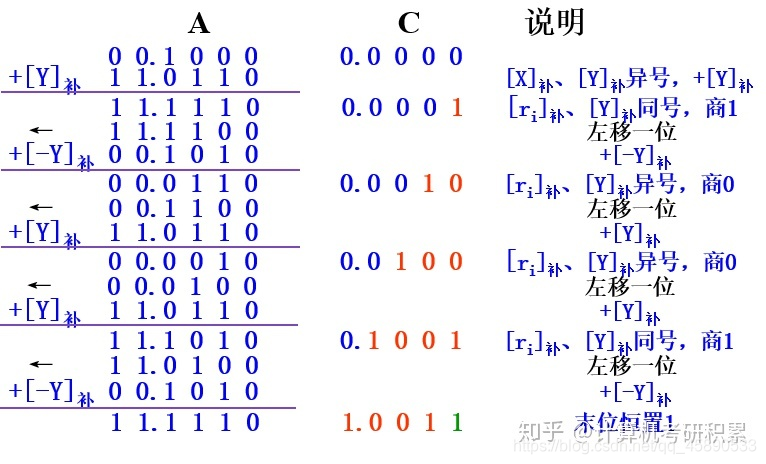
eg:p44

#### 4. Concept of Overflow and Detection Methods
##### Concept of Overflow
In fixed-point integer machines, the range of number representation is **|x| < (2^n^-1)**, if during operations a value exceeding the absolute value of the word length occurs, it is termed "overflow".
[Example 15] x=+1011 , y=+1001 , find x+y.
Solution: [x]_{two}=01011 , [y]_{two}=01001
[x]_{two} **0** 1 0 1 1
+ [y]_{two} **0** 1 0 0 1
——————————————
[x+y]_{two} **1** 0 1 0 0
The result of adding two positive numbers becomes negative, termed **overflow** (the result exceeds the maximum positive number representable by the machine).
[Example 16] x=-1101 , y=-1011 , find x+y.
Solution: [x]_{two}=10011 , [y]_{two}=10101
[x]_{two} **1** 0 0 1 1
+ [y]_{two} **1** 0 1 0 1
——————————————
[x+y]_{two} **0** 1 0 0 0
The result of adding two negative numbers becomes positive, termed **underflow** (the result is less than the minimum negative number representable by the machine).
##### Detection of Overflow
###### Double Sign Bit Method (Modified Two's Complement)
The numbers participating in addition and subtraction are represented using **modified two's complement**.
[x]_{two}=2^n+2^+x (mod 2^n+2^)
[x+y]_{two}=[x]_{two}+[y]_{two} (mod 2^n+2^)
- Both sign bits participate in the operation
- Under modulo 2^n+2, the carry generated by the highest sign bit is discarded
Sf1 SF2
0 0 Correct (Positive)
0 1 Overflow
1 0 Underflow
1 1 Correct (Negative)
**When the two sign bits differ**, it indicates **overflow**; **when they are the same**, **there is no overflow**. Regardless of whether there is overflow, **Sf1 (i.e., the highest bit) indicates the correct sign of the result**.
#### Exercises

## 2.3 Representation and Operations of Floating-Point Numbers
### 1. Representation of Floating-Point Numbers
Range of representation for floating-point numbers
### 2. IEEE754 Standard.
### 3. Addition and Subtraction of Floating-Point Numbers
1. Check for **zero operands**, to see if simplification is possible;
2. **Compare the exponents** and complete **alignment** (align the smaller exponent to the larger one);
3. Perform **addition or subtraction** on the **mantissas**;
4. **Normalize** the result and perform **rounding**.
#### Alignment
The process of making the exponents of the two numbers the same.
**Alignment Principle**: The number with the smaller exponent aligns with the number with the larger exponent.
**Alignment Process**: First, find the difference between the exponents E~x~ and E~y~ to see if they are equal. If not, adjust E~x~ and E~y~ by moving the mantissas, i.e., align them until they are equal. The mantissa of the smaller exponent is shifted right (equivalent to moving the decimal point left), and for each right shift, the exponent is increased by 1, until the exponents of the two numbers are equal, with the number of right shifts equal to the exponent difference.
#### Summation of Mantissas
The method is exactly the same as for fixed-point addition and subtraction.
#### Normalization
The normalization of floating-point numbers requires that **the most significant bit of the mantissa should be 1**, shifting the result **right** to achieve normalization is called **right normalization**, while shifting the result **left** to achieve normalization is called **left normalization**.
**Method for Judging Normalized Numbers** (Single Sign Method)
- Sign-Magnitude: Regardless of whether positive or negative, the first bit is 1
- One's Complement, Two's Complement: The sign bit and the first bit are different 
#### Rounding
The purpose of rounding: When aligning or normalizing to the right, the mantissa is shifted to the right, and the lower bits that are shifted out will be discarded, causing some error. To minimize the error.
Rounding according to the IEEE754 standard
- Round to nearest (0 rounds up 1 rounds down): Similar to "round half up", if the discarded highest bit is 1, round up.
- Round towards zero: Simple truncation
- Round towards +∞: If the extra bits are not all "0", round up; for negative numbers, truncate.
- Round towards -∞: If the extra bits are not all "0", round up; for positive numbers, truncate.



## 2.4 Arithmetic Logic Unit (ALU)
### 1. Serial and Parallel Adders
The logic expression for a one-bit full adder is as follows:
F~i~ = A~i~ ⊕ B~i~ ⊕ C~n+i~
C~n+i+1~ = A~i~B~i~ + A~i~C~n+i~ + B~i~C~n+i~
**C is the carry**
**Serial Adder**
- There is only one full adder, and data is sent to the adder bit by bit in series for computation. The carry flip-flop is used to store the carry signal for participation in the next computation.
- If the operands are n bits long, the addition must be performed n times, producing one sum bit each time, and the results are sent back to the register bit by bit in series.
**Parallel Adder**
- The parallel adder consists of multiple full adders, with the number of bits equal to the machine's word length, and all bits are computed simultaneously.
- The longest computation time for a parallel adder is mainly determined by the carry signal's propagation time.
- Each full adder in a parallel adder has a carry input from the lower bit and a carry output to the higher bit.
- The carry in a parallel adder is usually divided into serial carry and parallel carry.
### 2. Functions and Structure of the Arithmetic Logic Unit (ALU)
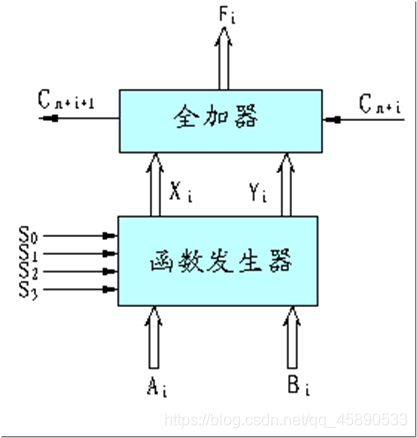
The logic diagram of the ALU is shown above.
F~i~ = X~i~ ⊕ Y~i~ ⊕ C~n+1~
C~n+i+1~ = X~i~Y~i~ + Y~i~C~n+1~ + X~i~C~n+1~
Different control parameters can yield different combinational functions, thus enabling various arithmetic and logical operations.
The relationship between Xi and Yi with the control parameters and input quantities is constructed as follows truth table.
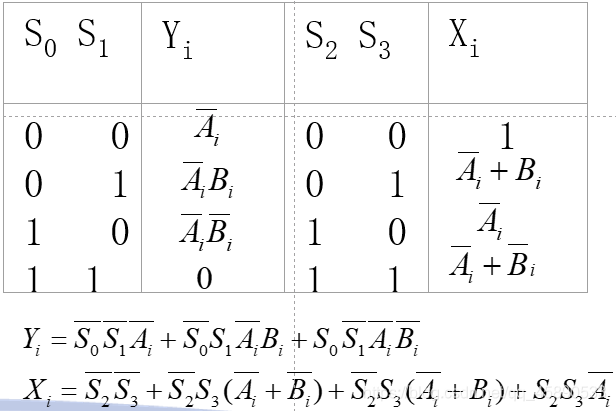
Loading...
Ownership of this post data is guaranteed by blockchain and smart contracts to the creator alone.