一、图#
1. 什么是图#
表示 “多对多” 的关系,包含了:
- 一组顶点:通常用 V (Vertex) 表示顶点集合
- 一组边:通常用 E (Edge) 表示边的集合
- 无向边是顶点对:(v,w) ∈ E,其中 v,w∈V
- 有向边 <v,w> 表示从 v 指向 w 的边 (单行线)
- 不考虑重边和自回路
抽象数据类型定义#
类型名称:图 (Graph)
数据对象集:G (V,E) 由一个非空的有限顶点集合 V 和一个有限边集合 E 组成。
操作集:对于任意图 G ∈ Graph, 以及 v ∈ V,e ∈ E
- Graph Create (): 建立并返回空图;
- Graph InsertVertex (Graph G, Vertex v):将 v 顶点插入图 G
- Graph InsertEdge (Graph G, Edge e): 将边 e 插入图 G
- void DFS (Graph G, Vertex v): 从顶点 v 出发深度优先遍历图 G;
- void BFS (Graph G, Vertex v): 从顶点 v 出发广度优先遍历图 G;
- void ShortestPath (Graph G, Vertex v, int Dist []): 计算图 G 中顶点 v 到其他任意顶点的最短距离;
- void MST (Graph G): 计算图 G 的最小生成树
常用术语:
无向图、有向图、网络等……
怎样在程序中表示图#
邻接矩阵#


邻接矩阵的好处
- 直观、简单、好理解
- 方便检查任意一对顶点间是否存在边
- 方便找任一顶点的所有 “邻接点”(有边直接相连的顶点)
- 方便计算任一顶点的 “度”(从该点发出的边数为 “出度”,指向该点的边数为 “入度”)
- 无向图为对应行 (或列) 非 0 元素的个数
- 有向图:对应行非 0 元素的个数是出度,对应列非 0 元素的个数是入度
邻接表#
指针数组 + 链表,点很稀疏的时候很合算

邻接表的好处:
- 方便找任一顶点的所有 “邻接点”(有边直接相连的顶点)
- 节约稀疏图的空间
- 需要 N 个头指针 + 2E 个结点(每个结点至少 2 个域)
- 方便计算无向图任一顶点的 “度”,但对有向图只能计算出度。
2. 图的遍历#
DFS 深度优先搜索#
深度优先搜索 (Depth First Search,DFS), 对每一个可能的分支路径深入到不能再深入为止,而且每个节点只能访问一次.
伪代码描述:
void DFS(Vertex V) {
visited[V] = true;
for(v的每个邻接点W)
if (!visited[W])
DFS(W);
}
BFS 广度优先搜索#
广度优先搜索 (Breadth First Search,BFS), 借助队列 (先进先出) 来实现
伪代码描述:
void BFS(Vertex V) {
visited[V] = true;
Enqueue(V, Q);//将该顶点放入队列中
while(!IsEmpty(Q)) {//当队列为空时结束搜索
V = Dequeue(Q);//V为队首元素
for(V的每个邻接点W) {
if ( !visited[W] ) {
visited[W] = true;//标记该点已访问
Enqueue(W, Q);//将该点压入队列中
}
}
}
}
图不连通怎么办?#
- 路径:V 到 W 的路径是一些列顶点 {V,V1,V2,……,Vn,W} 的集合,其中任一对相邻的顶点间都有图中的边。路径的长度是路径中的边数 (若带权,则是所有边的权重和)。若 V 到 W 之间的所有顶点都不同,则称为简单路径
- 连通:若 V 到 W 存在一条 (无向)路径,则称 V 和 W 是连通的
- 回路:起点等于终点的路径
- 连通图:图中任意两顶点均连通
- 连通分量:无向图的极大连通子图
- 极大顶点数:再加 1 个顶点就不连通了
- 极大边数:包含子图中所有顶点相连的所有边

- 强连通:有向图中顶点 V 和 W 之间存在双向路径,则称 V 和 W 是强连通的
- 强连通图:有向图中任意两顶点均强连通
- 强连通分量:有向图的极大强连通子图
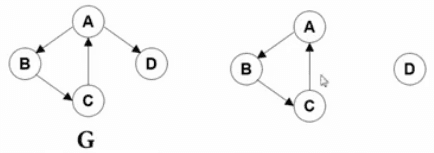
每调用一次 DFS,其实就是把 V 所在的连通分量遍历了一遍。BFS 也一样。
void ListComponents ( Graph G ) {//遍历连通分量
for (each V in G)
if ( !visited[V] ) {
DFS( V );
}
}
3. 如何建立图#
(1) 邻接矩阵表示的图的建立#
定义#
const int MaxVertexNum = 100;
typedef int DataType;
typedef bool WeightType;
typedef struct GNode *PtrToGNode;
struct GNode {
int Nv;//顶点数
int Ne;//边数
WeightType G[MaxVertexNum][MaxVertexNum];
DataType Data[MaxVertexNum];//存顶点的数据
};
typedef PtrToGNode MGraph;//以邻接矩阵存储的图类型
初始化#
初始化一个有 VertexNum 个顶点但没有边的图
typedef int Vertex;
MGraph CreateGraph(int VertexNum) {
Vertex V, W;
MGraph Graph;
Graph = (MGraph) malloc(sizeof(struct GNode));
Graph->Nv = VertexNum;
Graph->Ne = 0;
//顶点编号从0开始,到Graph->Nv-1
for (V = 0; V < Graph->Nv; V++) {
for(W = 0; W < Graph->Nv; W++) {
Graph->G[V][W] = 0; //有向图中可改0为INF等
}
}
return Graph;
}
向图中插入边#
边的定义
typedef struct ENode *PtrToENode;
struct ENode {
Vertex V1, V2;//有向边<V1,V2>
WeightType Weight;//权重
};
typedef PtrToENode Edge;
插入操作
void InsertEdge(MGraph Graph, Edge E) {
//插入边<V1,V2>
Graph->G[E->V1][E->V2] = E->Weight;
//若为无向图,则还要插入边<V2,V1>
Graph->G[E->V2][E->V1] = E->Weight;
}
完整的建立一个 MGraph#
输入格式
Nv Ne
V1 V2 Weight
……
MGraph BuildGraph() {
MGraph Graph;
Edge E;
Vertex V;
int Nv;
cin >> Nv;
Graph = CreateGraph(Nv);//建立有Nv个顶点的图
cin >> Graph->Ne;//边数Ne
if(Graph->Ne != 0) {
E = (Edge)malloc(sizeof(struct ENode));
for (int i = 0; i < Graph->Ne; i++) {
cin >> E->V1 >> E->V2 >> E->Weight;
InsertEdge(Graph, E);
}
}
//如果顶点有数据的话,读入数据
for(V = 0; V < Graph->Nv; V++) {
cin >> Graph->Data[V];
}
return Graph;
}
(2) 邻接表表示的图的建立#
可在邻接矩阵的基础上进行修改
定义#
const int MaxVertexNum = 100;
typedef int DataType;
typedef int Vertex;
typedef bool WeightType;
//邻接表定义
typedef struct AdjVNode *PtrToAdjVNode;
struct AdjVNode {
Vertex AdjV;//邻接点下标
WeightType Weight;//边权重
PtrToAdjVNode Next;
};
typedef struct VNode {
PtrToAdjVNode FirstEdge;
DataType Data;//存顶点的数据
}AdjList;
typedef struct GNode *PtrToGNode;
struct GNode {
int Nv;//顶点数
int Ne;//边数
AdjList G;//邻接表
};
typedef PtrToGNode LGraph;//以邻接表存储的图类型
LGraph 初始化#
LGraph CreateGraph(int VertexNum) {
Vertex V, W;
LGraph Graph;
Graph = (LGraph) malloc(sizeof(struct GNode));
Graph->Nv = VertexNum;
Graph->Ne = 0;
//顶点编号从0开始,到Graph->Nv-1
for (V = 0; V < Graph->Nv; V++) {
Graph->G[V].FirstEdge = NULL;
return Graph;
}
向 LGraph 中插入边#
typedef struct ENode *PtrToENode;
struct ENode {
Vertex V1, V2;//有向边<V1,V2>
WeightType Weight;//权重
};
typedef PtrToENode Edge;
void InsertEdge(LGraph Graph, Edge E){
PtrToAdjVNode NewNode;
//插入边<V1,V2>
//为V2建立新的邻接点
NewNode = (PtrToAdjVNode) malloc(sizeof(struct AdjVNode));
NewNode->AdjV = E->V2;
NewNode->Weight = E->Weight;
//将V2邻接点插入V1的表头
NewNode->Next = Graph->G[E->V1].FirstEdge;
Graph->G[E->V1].FirstEdge = NewNode;
//若为无向图 则还要插入边<V2,V1>
//为V2建立新的邻接点
NewNode = (PtrToAdjVNode) malloc(sizeof(struct AdjVNode));
NewNode->AdjV = E->V1;
NewNode->Weight = E->Weight;
//将V2邻接点插入V1的表头
NewNode->Next = Graph->G[E->V2].FirstEdge;
Graph->G[E->V1].FirstEdge = NewNode;
}
完整的建立一个 LGraph#
仅需将 MGraph 换成 LGraph,将存 Data 是稍作更改即可
LGraph BuildGraph() {
LGraph Graph;
Edge E;
Vertex V;
int Nv;
cin >> Nv;
Graph = CreateGraph(Nv);//建立有Nv个顶点的图
cin >> Graph->Ne;//边数Ne
if(Graph->Ne != 0) {
E = (Edge)malloc(sizeof(struct ENode));
for (int i = 0; i < Graph->Ne; i++) {
cin >> E->V1 >> E->V2 >> E->Weight;
InsertEdge(Graph, E);
}
}
//如果顶点有数据的话,读入数据
for(V = 0; V < Graph->Nv; V++) {
cin >> Graph->G[V].Data;
}
return Graph;
}
二、最短路径问题#
1. 概念简介#
- 在网络中,求两个不同顶点之间的所有路径中,边的权值之和最小的那一条路径
- 这条路径就是两点之间的最短路径 (Shortest Path)
- 第一个顶点叫源点 (Source)
- 最后一个顶点叫终点 (Destination)
2. 问题分类#
- 单源最短路径问题:从某固定源点出发,求其到所有其他顶点的最短路径
- (有向) 无权图
- (有向) 有权图
- 多源最短路径问题:求任意两顶点之间的最短路径
2. 无权图的单源最短路算法#
按照递增的顺序找出到各个顶点的最短路,与 BFS 思想很类似!
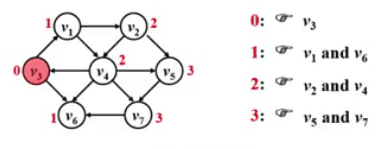
首先需要定义一个数组 dist,dist [W] 存储 S 到 W 的最短距离,S 为起点,dist [S]=0,dist 需要被初始化成一个 - 1 (或无穷),便于后来的判别是否被访问过。
其次需要定义数组 path,path [W] 存储 S 到 W 的路上经过的某顶点。
dist 和 path 数组都需先被初始化为 - 1~ 然后将起点的 dist [S] 设为 0,压入队列开始访问
伪代码:
void Unweighted(Vertex S) {
Enqueue(S, Q);
while(!IsEmpty(Q)) {
V = Dequeue(Q);
for (V的每个邻接点W)
if(dist[W] == -1) {
dist[W] = dist[V]+1;
path[W] = V;
Enqueue(W, Q);
}
}
}
3. 有权图的单源最短路算法#
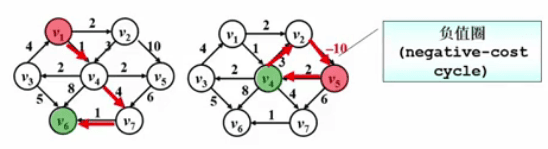
Dijkstra 算法!#
- 令 s={源点 s + 已经确定了最短路径的顶点 v~i~}
- 对任一未收录的顶点 v 定义 dist [v] 为 s 到 v 的最短路径长度,但该路径仅经过 S 中的顶点,即路径 {s→(v~i~∈S)→v} 的最小长度
- 若路径是按照递增的顺序生成的,则
- 真正的最短路必须只经过 S 中的顶点 (反证法可证)
- 每次从未收录的顶点中选一个 dist 最小的收录 (贪心)
- 增加一个 v 进入 S, 可能会影响另外一个 w 的 dist 值!(所以要检查 v 的所有邻接点 w!)
- dist [w] = min { dist [w],dist [v] + <v,w > 的权重}
dist 初始化:S 的所有邻接点 W 的 dist 都可初始化为 s 与 w 的权重,其他则定义为正无穷。
- dist [w] = min { dist [w],dist [v] + <v,w > 的权重}
伪代码描述:
void Dijkstra(Vertex s) {
while (1){
V = 未收录顶点中dist最小者;
if (这样的V不存在)
break;
collected[V] = true;
for (V的每个邻接点W)
if(collected[W] == false)
if(dist[V] + E<v,w> < dist[W]) {
dist[W] = dist[V]+E<v,w>;
path[W] = V;
}
}
}//不能解决有负边的情况
伪代码中 dist [W]=dist [V]+E~<V,W>~;并不是简单的赋值,而是如果有了更短的距离,需要将其更新成为更短的距离

Dijkstra 核心代码#
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
using namespace std;
const int maxn = 1005;
const int inf = 0x3f3f3f;
int T,N,x,y,z;
int edge[maxn][maxn];
int dist[maxn];
bool vis[maxn];
void init() {
for(int i = 1; i <= N; ++i) {
for(int j = 1; j <= N; ++j) {
edge[i][j] = inf;
}
edge[i][i] = 0;
}
}
void Dijstra(int u) {
for(int i = 1; i <= N; ++i) {
vis[i] = false;
dist[i] = edge[u][i];
}
vis[u] = true;
for(int i = 1; i <= N; ++i) {
int t, mindis = inf;
for(int j = 1; j <= N; ++j) {
if(!vis[j] && dist[j] < mindis) {
mindis = dist[j];
t = j;
}
}
vis[t] = true;
for(int j = 1; j <= N; ++j)
if(!vis[j] && dist[j] > edge[t][j] + dist[t])
dist[j] = edge[t][j] + dist[t];
}
}
三、最小生成树#
1. 什么是最小生成树 (Minimum Spanning Tree)#
- 是一棵树
- 无回路
- |V | 个顶点一定有 | V|-1 条边
- 是生成树
- 包含全部顶点
- |V|-1 条边都在图里
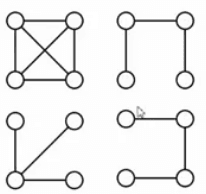
- 向生成树中任加一条边都一定构成回路
- 边的权重和最小
最小生成树与图连通等价
2. 解决最小生成树问题#
通常离不开贪心算法:
- “贪”:每一步都要最好的
- “好”:权重最小的边
- 需要约束:
- 只能用图里有的边
- 只能正好用掉 | V|-1 条边
- 不能有回路
放到了另一篇博客里。
图论 —— 解决最小生成树问题 (Kruskal 算法 & Prim 算法)