数据结构学习笔记＜7＞图

一、图#

1. 什么是图#

表示 “多对多” 的关系，包含了：

一组顶点：通常用 V (Vertex) 表示顶点集合
一组边：通常用 E (Edge) 表示边的集合
无向边是顶点对：(v，w) ∈ E，其中 v，w∈V
有向边 <v,w> 表示从 v 指向 w 的边 (单行线)
不考虑重边和自回路

抽象数据类型定义#

类型名称：图 (Graph)
数据对象集：G (V,E) 由一个非空的有限顶点集合 V 和一个有限边集合 E 组成。
操作集：对于任意图 G ∈ Graph, 以及 v ∈ V，e ∈ E

Graph Create (): 建立并返回空图；
Graph InsertVertex (Graph G, Vertex v)：将 v 顶点插入图 G
Graph InsertEdge (Graph G, Edge e): 将边 e 插入图 G
void DFS (Graph G, Vertex v): 从顶点 v 出发深度优先遍历图 G；
void BFS (Graph G, Vertex v): 从顶点 v 出发广度优先遍历图 G；
void ShortestPath (Graph G, Vertex v, int Dist []): 计算图 G 中顶点 v 到其他任意顶点的最短距离；
void MST (Graph G): 计算图 G 的最小生成树
常用术语：
无向图、有向图、网络等……

怎样在程序中表示图#

邻接矩阵#

在这里插入图片描述

邻接矩阵的好处

直观、简单、好理解
方便检查任意一对顶点间是否存在边
方便找任一顶点的所有 “邻接点”(有边直接相连的顶点)
方便计算任一顶点的 “度”(从该点发出的边数为 “出度”，指向该点的边数为 “入度”)
- 无向图为对应行 (或列) 非 0 元素的个数
- 有向图：对应行非 0 元素的个数是出度，对应列非 0 元素的个数是入度

邻接表#

指针数组 + 链表，点很稀疏的时候很合算
在这里插入图片描述
邻接表的好处：

方便找任一顶点的所有 “邻接点”(有边直接相连的顶点)
节约稀疏图的空间
- 需要 N 个头指针 + 2E 个结点（每个结点至少 2 个域）
方便计算无向图任一顶点的 “度”，但对有向图只能计算出度。

2. 图的遍历#

DFS 深度优先搜索#

深度优先搜索 (Depth First Search,DFS), 对每一个可能的分支路径深入到不能再深入为止，而且每个节点只能访问一次.
伪代码描述：

void DFS(Vertex V) {
	visited[V] = true;
	for(v的每个邻接点W)
		if (!visited[W])
			DFS(W);
}

BFS 广度优先搜索#

广度优先搜索 (Breadth First Search,BFS), 借助队列 (先进先出) 来实现
伪代码描述：

void BFS(Vertex V) {
	visited[V] = true;
	Enqueue(V, Q);//将该顶点放入队列中
	while(!IsEmpty(Q)) {//当队列为空时结束搜索
		V = Dequeue(Q);//V为队首元素
		for(V的每个邻接点W) {
			if ( !visited[W] ) {
				visited[W] = true;//标记该点已访问
				Enqueue(W, Q);//将该点压入队列中
			}
		}
	}
}

图不连通怎么办？#

路径：V 到 W 的路径是一些列顶点 {V，V1，V2，……，Vn，W} 的集合，其中任一对相邻的顶点间都有图中的边。路径的长度是路径中的边数 (若带权，则是所有边的权重和)。若 V 到 W 之间的所有顶点都不同，则称为简单路径
连通：若 V 到 W 存在一条 (无向)路径，则称 V 和 W 是连通的
回路：起点等于终点的路径
连通图：图中任意两顶点均连通
连通分量：无向图的极大连通子图
- 极大顶点数：再加 1 个顶点就不连通了
- 极大边数：包含子图中所有顶点相连的所有边
强连通：有向图中顶点 V 和 W 之间存在双向路径，则称 V 和 W 是强连通的
强连通图：有向图中任意两顶点均强连通
强连通分量：有向图的极大强连通子图

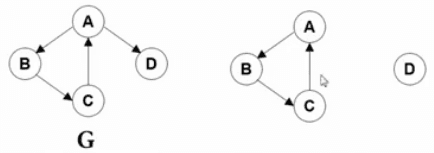
每调用一次 DFS，其实就是把 V 所在的连通分量遍历了一遍。BFS 也一样。

void ListComponents ( Graph G ) {//遍历连通分量
	for (each V in G)
		if ( !visited[V] ) {
			DFS( V );
		}
}

3. 如何建立图#

(1) 邻接矩阵表示的图的建立#

定义#

const int MaxVertexNum = 100;
typedef int DataType;
typedef bool WeightType;
typedef struct GNode *PtrToGNode;
struct GNode {
    int Nv;//顶点数
    int Ne;//边数
    WeightType G[MaxVertexNum][MaxVertexNum];
    DataType Data[MaxVertexNum];//存顶点的数据
};
typedef PtrToGNode MGraph;//以邻接矩阵存储的图类型

初始化#

初始化一个有 VertexNum 个顶点但没有边的图

typedef int Vertex;
MGraph CreateGraph(int VertexNum) {
    Vertex V, W;
    MGraph Graph;
    Graph = (MGraph) malloc(sizeof(struct GNode));
    Graph->Nv = VertexNum;
    Graph->Ne = 0;
    //顶点编号从0开始，到Graph->Nv-1
    for (V = 0; V < Graph->Nv; V++) {
        for(W = 0; W < Graph->Nv; W++) {
            Graph->G[V][W] = 0; //有向图中可改0为INF等
        }
    }
    return Graph;
}

向图中插入边#

边的定义

typedef struct ENode *PtrToENode;
struct ENode {
    Vertex V1, V2;//有向边<V1,V2>
    WeightType Weight;//权重
};
typedef PtrToENode Edge;

插入操作

void InsertEdge(MGraph Graph, Edge E) {
    //插入边<V1,V2>
    Graph->G[E->V1][E->V2] = E->Weight;
    //若为无向图，则还要插入边<V2,V1>
    Graph->G[E->V2][E->V1] = E->Weight;
}

完整的建立一个 MGraph#

输入格式

Nv Ne
V1 V2 Weight
……

MGraph BuildGraph() {
    MGraph Graph;
    Edge E;
    Vertex V;
    int Nv;
    cin >> Nv;
    Graph = CreateGraph(Nv);//建立有Nv个顶点的图
    cin >> Graph->Ne;//边数Ne
    if(Graph->Ne != 0) {
        E = (Edge)malloc(sizeof(struct ENode));
        for (int i = 0; i < Graph->Ne; i++) {
            cin >> E->V1 >> E->V2 >> E->Weight;
            InsertEdge(Graph, E);
        }
    }
    //如果顶点有数据的话，读入数据
    for(V = 0; V < Graph->Nv; V++) {
        cin >> Graph->Data[V];
    }
    return Graph;
}

(2) 邻接表表示的图的建立#

可在邻接矩阵的基础上进行修改

定义#

const int MaxVertexNum = 100;
typedef int DataType;
typedef int Vertex;
typedef bool WeightType;
//邻接表定义
typedef struct AdjVNode *PtrToAdjVNode;
struct AdjVNode {
    Vertex AdjV;//邻接点下标
    WeightType Weight;//边权重
    PtrToAdjVNode Next;
};

typedef struct VNode {
    PtrToAdjVNode FirstEdge;
    DataType Data;//存顶点的数据
}AdjList;

typedef struct GNode *PtrToGNode;
struct GNode {
    int Nv;//顶点数
    int Ne;//边数
    AdjList G;//邻接表
};
typedef PtrToGNode LGraph;//以邻接表存储的图类型

LGraph 初始化#

LGraph CreateGraph(int VertexNum) {
    Vertex V, W;
    LGraph Graph;
    Graph = (LGraph) malloc(sizeof(struct GNode));
    Graph->Nv = VertexNum;
    Graph->Ne = 0;
    //顶点编号从0开始，到Graph->Nv-1
    for (V = 0; V < Graph->Nv; V++) {
        Graph->G[V].FirstEdge = NULL;
    return Graph;
}

向 LGraph 中插入边#

typedef struct ENode *PtrToENode;
struct ENode {
    Vertex V1, V2;//有向边<V1,V2>
    WeightType Weight;//权重
};
typedef PtrToENode Edge;
void InsertEdge(LGraph Graph, Edge E){
    PtrToAdjVNode NewNode;
    //插入边<V1,V2>
    //为V2建立新的邻接点
    NewNode = (PtrToAdjVNode) malloc(sizeof(struct AdjVNode));
    NewNode->AdjV = E->V2;
    NewNode->Weight = E->Weight;
    //将V2邻接点插入V1的表头
    NewNode->Next = Graph->G[E->V1].FirstEdge;
    Graph->G[E->V1].FirstEdge = NewNode;
    
    //若为无向图 则还要插入边<V2,V1>
    //为V2建立新的邻接点
    NewNode = (PtrToAdjVNode) malloc(sizeof(struct AdjVNode));
    NewNode->AdjV = E->V1;
    NewNode->Weight = E->Weight;
    //将V2邻接点插入V1的表头
    NewNode->Next = Graph->G[E->V2].FirstEdge;
    Graph->G[E->V1].FirstEdge = NewNode;
}

完整的建立一个 LGraph#

仅需将 MGraph 换成 LGraph，将存 Data 是稍作更改即可

LGraph BuildGraph() {
    LGraph Graph;
    Edge E;
    Vertex V;
    int Nv;
    cin >> Nv;
    Graph = CreateGraph(Nv);//建立有Nv个顶点的图
    cin >> Graph->Ne;//边数Ne
    if(Graph->Ne != 0) {
        E = (Edge)malloc(sizeof(struct ENode));
        for (int i = 0; i < Graph->Ne; i++) {
            cin >> E->V1 >> E->V2 >> E->Weight;
            InsertEdge(Graph, E);
        }
    }
    //如果顶点有数据的话，读入数据
    for(V = 0; V < Graph->Nv; V++) {
        cin >> Graph->G[V].Data;
    }
    return Graph;
}

二、最短路径问题#

1. 概念简介#

在网络中，求两个不同顶点之间的所有路径中，边的权值之和最小的那一条路径
- 这条路径就是两点之间的最短路径 (Shortest Path)
- 第一个顶点叫源点 (Source)
- 最后一个顶点叫终点 (Destination)

2. 问题分类#

单源最短路径问题：从某固定源点出发，求其到所有其他顶点的最短路径
- (有向) 无权图
- (有向) 有权图
多源最短路径问题：求任意两顶点之间的最短路径

2. 无权图的单源最短路算法#

按照递增的顺序找出到各个顶点的最短路，与 BFS 思想很类似！
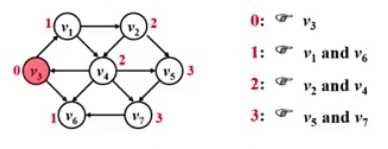
在这里插入图片描述
首先需要定义一个数组 dist,dist [W] 存储 S 到 W 的最短距离，S 为起点，dist [S]=0，dist 需要被初始化成一个 - 1 (或无穷)，便于后来的判别是否被访问过。
其次需要定义数组 path,path [W] 存储 S 到 W 的路上经过的某顶点。
dist 和 path 数组都需先被初始化为 - 1~ 然后将起点的 dist [S] 设为 0，压入队列开始访问
伪代码：

void Unweighted(Vertex S) {
	Enqueue(S, Q);
	while(!IsEmpty(Q)) {
		V = Dequeue(Q);
		for (V的每个邻接点W)
			if(dist[W] == -1) {
				dist[W] = dist[V]+1;
				path[W] = V;
				Enqueue(W, Q);
			}
	}
}

3. 有权图的单源最短路算法#

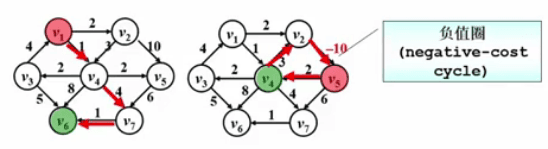
在这里插入图片描述

Dijkstra 算法！#

令 s={源点 s + 已经确定了最短路径的顶点 v~i~}
对任一未收录的顶点 v 定义 dist [v] 为 s 到 v 的最短路径长度，但该路径仅经过 S 中的顶点，即路径 {s→(v~i~∈S)→v} 的最小长度
若路径是按照递增的顺序生成的，则
- 真正的最短路必须只经过 S 中的顶点 (反证法可证)
- 每次从未收录的顶点中选一个 dist 最小的收录 (贪心)
- 增加一个 v 进入 S, 可能会影响另外一个 w 的 dist 值！(所以要检查 v 的所有邻接点 w！)
  - dist [w] = min { dist [w]，dist [v] + <v,w > 的权重}
    dist 初始化：S 的所有邻接点 W 的 dist 都可初始化为 s 与 w 的权重，其他则定义为正无穷。

伪代码描述：

void Dijkstra(Vertex s) {
	while (1){
		V = 未收录顶点中dist最小者;
		if (这样的V不存在)
			break;
		collected[V] = true;
		for (V的每个邻接点W)
			if(collected[W] == false)
				if(dist[V] + E<v,w> < dist[W]) {
					dist[W] = dist[V]+E<v,w>;
					path[W] = V;
				}
	}
}//不能解决有负边的情况

伪代码中 dist [W]=dist [V]+E~<V,W>~；并不是简单的赋值，而是如果有了更短的距离，需要将其更新成为更短的距离
在这里插入图片描述

Dijkstra 核心代码#

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
using namespace std;
const int maxn = 1005;
const int inf  = 0x3f3f3f;
int T,N,x,y,z;
int edge[maxn][maxn];
int dist[maxn];
bool vis[maxn];
void init() {
    for(int i = 1; i <= N; ++i) {
        for(int j = 1; j <= N; ++j) {
            edge[i][j] = inf;
        }
        edge[i][i] = 0;
    }
}
void Dijstra(int u) {
    for(int i = 1; i <= N; ++i) {
        vis[i] = false;
        dist[i] = edge[u][i];
    }
    vis[u] = true;
    for(int i = 1; i <= N; ++i) {
        int t, mindis = inf;
        for(int j = 1; j <= N; ++j) {
            if(!vis[j] && dist[j] < mindis) {
                mindis = dist[j];
                t = j;
            }
        }
        vis[t] = true;
        for(int j = 1; j <= N; ++j) 
            if(!vis[j] && dist[j] > edge[t][j] + dist[t]) 
                dist[j] = edge[t][j] + dist[t];
    }
}

三、最小生成树#

1. 什么是最小生成树 (Minimum Spanning Tree)#

是一棵树
- 无回路
- |V | 个顶点一定有 | V|-1 条边
是生成树
- 包含全部顶点
- |V|-1 条边都在图里
- 向生成树中任加一条边都一定构成回路
边的权重和最小

最小生成树与图连通等价

2. 解决最小生成树问题#

通常离不开贪心算法：

“贪”：每一步都要最好的
“好”：权重最小的边
需要约束：
- 只能用图里有的边
- 只能正好用掉 | V|-1 条边
- 不能有回路

放到了另一篇博客里。
图论 —— 解决最小生成树问题 (Kruskal 算法 & Prim 算法)